Houdini Curve Decimation
Last updated on: 2 December, 2022
Problem Description
One day when I was working on a subdivision model based mostly on shapes built from curves, I decided that it’s about time to look for some proper way of decimating curves. The method I was looking for should be capable of reducing the number of points in a resampled Bézier spline while at the same time preserving points where they are most needed (in areas of high curvature), and keep the shape of a new curve as much close to the original as possible.
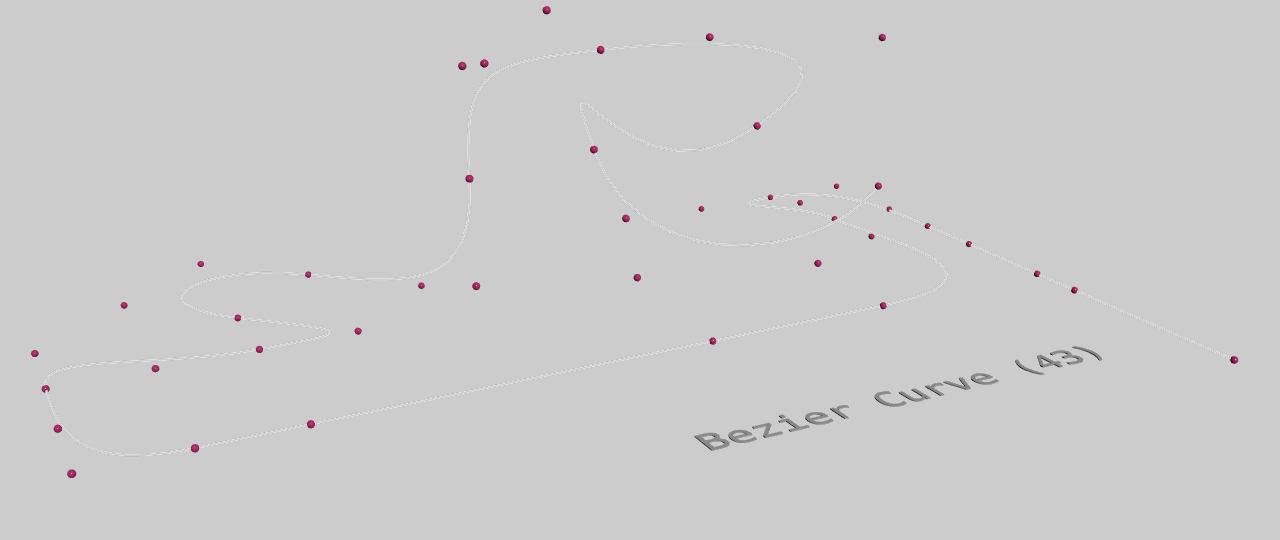
Our input: 49-points of pure Bézier curve.
All methods described here require discrete splines as their inputs, so NURBS and Bézier curves must first be resampled to polylines. The greater the point count, the more the discrete curve will follow the original parametric shape and the more data we have to operate on. Naturally, it’s best to keep the point count at subjectively sane levels. Usually I look for curve’s finest features and then decrease maximum segment length until the curve becomes smooth enough in those parts.
Bézier curve resampled to 3024 points (magenta spheres) and visualization of its curvature.
Two Most Common Methods
I found a handful of threads on SideFX forum in which people are asking for a way of decimating curves in Houdini. Most of those threads conclude in a recommendation of two main methods:
- Using Refine SOP.
- Using PolyReduce SOP.
The first one I have already known and is the method I’ve been using for a long time. It’s very fast and offers passable results, but often it produces points in areas where it’s not necessary, while those points could be used to better maintain curvature in other parts of the spline.
Unrefining the curve.
This problem can be seen in the upper area of the curve from the animation above. As the point count decreases, a short part of the curve is increasingly being offset from the original shape due to lack of points that could sustain that shape. At the same time, other areas receive way to many points. Depending on our goal and the curve itself, this might or might not be acceptable.
The method boils down to dropping a “Refine SOP” on a resampled curve, setting first and second U to (0, 1) in order to affect the whole curve length, and finally enabling the Unrefine action. The greater the value of Tolerance U (tolu), the bigger decimation level of a curve we get. This parameter is dependent of input curve resolution and is very sensitive. Start from zero, then proceed in tiny fractions to greater values.
About the other method I did not know before, so I was quite surprised reading that PolyReduce can actually operate on poly curves, as I never could make it work on them. It turned out that it does, but input splines must be closed first before they’re fed to this operator.
Point reduction with PolyReduce SOP.
While closing curves can be easily achieved with Ends SOP, using PolyReduce to decimate curves introduces a lot of problems. The operator presents a very strong tendency of clumping points in straight areas and in general in what feels like random parts of the curve. It’s not as evident on circular closed curves than it is on relatively straight open, or complex splines. Therefore, while it might be useful in some circumstances, I’m not a big fan of this method.
Mathematical Algorithms
I continued with my search for a better way of decimating curves, but this time I focused on existing mathematical algorithms. It turned out there are quite a few, but two of them seemed to be the most popular:
- Ramer-Douglas-Peucker’s (RDP),
- Visvalingam-Whyatt’s.
Both are widely used in cartography. The first comes from around 1972-1973 and uses divide-and-conquer approach, while the other one is a bit younger (I think it was first proposed in 1992) and is based on areas of triangles. Michael Barry has a very good side-by-side comparison of both algorithms in action. It shows that both algorithms are equally good at converging on the original curve shape, just in a slightly different way.
So far I only tested Ramer-Douglas-Peucker from a prosaic reason of it popping up more frequently in the search engine. The results in Houdini are immensely better than what is offered by methods described earlier in the post.
Animation of curve decimation with Ramer-Douglas-Peucker algorithm. Reduction from 3023 to 130 points (Ɛ = 0 to Ɛ = 0.01).
I’ve used Fabian Hirschmann’s Python implementation, which pretty much works out-of-the-box. It comes with an iterative and recursive versions of the RDP algorithm. If you want to incorporate this implementation into your workflow, simply paste Fabian’s code into a Python SOP and feed it with data from hou.Geometry object you’re processing.
Some hints:
Mis an ordered point set, so it’shou.pwd().geometry.points().- Read
epsilonfrom a parameter. - Remove all Docstrings, or otherwise Python SOP won’t work for some reason.
And a spoiler:
# Fabian's code goes here.
# (...)
node = hou.pwd()
geo = node.geometry()
M = []
points = geo.points()
for point in points:
print(point.position())
M.append(point.position())
reduced = rdp(M, epsilon=node.parm("epsilon").eval())
geo.deletePrims(geo.prims())
geo.createPoints(reduced)
This will return an ordered point set from which we can then create a curve primitive straight from a detail wrangle:
int points[];
for(int i=0; i<npoints(0); i++){
push(points, i);
}
addprim(0, "polyline", points);
The only disadvantage of this solution that I’ve noticed so far, is that decimation is very slow. On my current workstation it takes about 2.3 seconds to reduce a curve from 3023 to 130 points using iterative algorithm (recursive algorithm is about 100ms slower). That’s A LOT of processing time if you ask me, especially considering that Unrefine, for instance, only needs less than 1 millisecond to decimate the same curve, and that RDP has worst case complexity of $\theta(n^2)$1, so it shouldn’t be THAT bad. It might be the implementation, it might be the slowness of Python SOP. I don’t have time to investigate. If this becomes a nuisance, I might take a closer look at the code, or perhaps try to reimplement the algorithm in VEX at some point, in order to see if this would speed things up. But currently I’m very happy with what I have.
Further Readings
- David H. Douglas, Thomas K. Peucker. Algorithms for the Reduction of The Number of Points Required to Represent a Digitized Line of Its Caricature. The Canadian Cartographer Vol. 10 No. 2, 2 December 1973. DOI:10.3138/FM57-6770-U75U-7727.
- Urs Ramer. An Iterative Procedure for the Polygonal Approximation of Plane Curves. Computer Graphics And Image Processing Vol. 1 (1972). DOI:10.1016/S0146-664X(72)80017-0.
- M. Visvalingam, J. D. Whyatt. Line Generalisation by Repeated Elimination of the Smallest Area. Cartographic Information Systems Research Group C.I.S.R.G Discussion Paper 10, July 1992 (Link).
- 2IMA20 Algorithms for Geographic Data, Lecture 5: Simplification. Technische Universiteit Eindhoven (2016) (Link).
-
RDP’s best case time complexity is $O(n\log{n})$. ↩︎